Необходимость введения нового Федерального государственного образовательного стандарта (ФГОС) ‒ это веление времени. ФГОС предусматривает задание ориентиров развития всего образовательного пространства в интересах государства, общества, семьи и личности.

Выбирая среди большого количества различных технологий, которые применяются в системе образования, необходимо уделить внимание новациям, где учитель является не только источником информации, а также координатором и организатором учебной деятельности направляя учеников в нужное русло, в зависимости от их индивидуальных способностей.

Учебно-познавательная задача это часть содержания образования учебного материала, задача, которая изучает объект или помогает усвоить новые знания о нём. Это задача, содержащая в себе затруднения, она создается во имя открытия и развития нового знания. Для её решения необходимо развивать у учащихся наглядно-образное мышление.

Обучение математике без наглядности невозможно. Наглядность это самый известный и распространенный инструмент в педагогике. Сравнительно недавно, учёные установили, что у большинства людей наибольшей восприимчивостью обладают органы зрения, которые «проводят» в мозг почти в 5 раз больше информации, чем органы слуха, и почти в 13 раз больше, чем органы осязания.

Одна из программ удобная для учителей математики - GeoGebra, она позволяет быстро создавать наглядный материал, интерактивные чертежи и пользоваться большим собранием уже созданных ресурсов. 

Естественно, что в классе всегда есть дети с различными способностями и уровнем подготовки, с разными возможностями воспринимать материал. Поэтому используя СПО GeoGebra на уроках, можно обеспечить необходимое количество наглядного материала. Сделать это совсем просто, если появляется необходимость изменить материал, в зависимости от восприятия учащимися материала, это можно сделать прямо на уроке, как самому учителю, так и учащимся. Для уроков математики и геометрии можно построить чертежи любой степени сложности. На уроках алгебры можно легко составлять графики функций, подбирая необходимые параметры, менять их в зависимости от условия задачи. Примечательная особенность в GeoGebra - двойное представление объектов: каждое выражение в окне алгебры соответствует объекту в окне геометрии и наоборот.

 

 

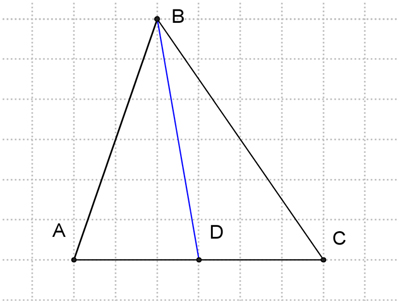
Привожу небольшую учебно-познавательную задачу, решаемую на уроке геометрии, при помощи программы GeoGebra.

 

Название задачи: Построение биссектрисы, высоты, медианы треугольника.

Тип задачи: обобщающее-обучающая задача

Учебные дисциплины: геометрия, информатика

7 класс 

Текст задачи: Используя возможности программы GeoGebra построить и доказать, что отрезок BD является биссектрисой, медианой, высотой

Основные действия учеников на каждом из этапов решения задачи:

1 этап. Осмысление условия 

– Осуществить отбор актуальной информации по чертежу.

– Выделить ключевые элементы задачи и их отношения (биссектриса ↔ угол пополам, медиана ↔ середина стороны, высота ↔ перпендикуляр ↔ прямой угол).

– Соотнести известные и неизвестные элементы задачи.

– Распознать известные элементы и их  сочетания.

– Зафиксировать условия в виде краткой записи (чертежа).

2 этап. Составление плана решения

Разбить данную задачу на подзадачи и сформулировать их.

3 этап. Осуществление плана решения

Решение 1 подзадачи

Построение медианы. На данном рисунке построена медиана, дать определение, посчитать по клеткам отрезок AD и DC.

 

Решение 2 подзадачи

 

 

 

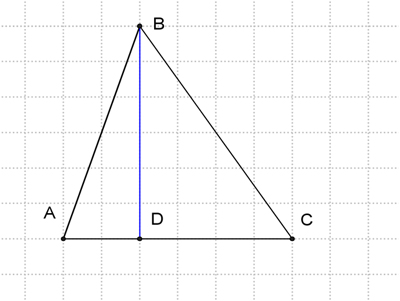
Построение высоты. Перемещение точки D таким образом, чтобы угол BDC получился прямым, используя клетки.

Решение 3 подзадачи

 

 

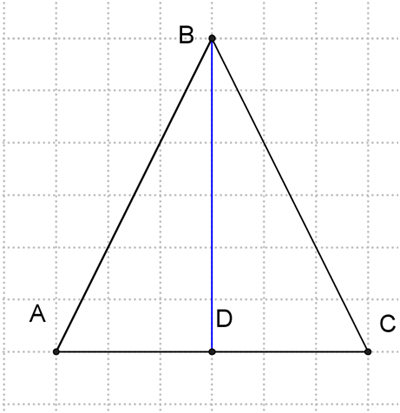
– Построение биссектрисы. На данном этапе построить биссектрису можно только примерно, но изменив треугольник на равнобедренный, можно использовать свойство биссектрисы, медианы и высоты проведенной к основанию.

Изучение найденного решения 

– Вспомнить все определения и понятия, используемые при решении, предположить какое является самым «простым» (индивидуальная работа и работа в парах, при желании можно озвучить всему классу).

– В качестве дополнительного задания можно предложить, дома используя программу GeoGebra построить данные величины в треугольниках, где один угол прямой, тупой. Проще или сложнее станет от этого задача.

Образовательные результаты (без учета дополнительных вопросов):

1. Предметные: 

Геометрия: построение основных характеристик в геометрии, используя клетки.

Информатика: работа с чертежом на компьютере.

2. Метапредметные: 

Познавательные учебные действия:

– структурировать информацию и представлять ее в понятной форме;

– строить логические цепочки;

– давать определение понятиям;

– делать выводы и умозаключения.

Коммуникативные учебные действия:

– с достаточной точностью и полнотой выражать свои мысли и подбирать аргументы, доказывающие, что построенный отрезок является искомым.

Регулятивные учебные действия:

– соотносить учебные действия с известным определением;

3. Личностные: 

– выстраивать аргументацию;

– проявлять находчивость и активность при решении задачи;

– воспринимать объекты окружающего мира через сравнение и сопоставление величин, их характеризующих.

Представленная схема анализа учебно-познавательной задачи позволяет сделать вывод о том, какими именно действиями овладеют обучающиеся в процессе решения конкретной задачи: познавательными, личностными, регулятивными, коммуникативными,  а также позволяет учителю объективно спрогнозировать образовательные эффекты в процессе решения данной учебно-познавательной задачи [2].

 

Список литературы

1. Абдулаева О.А. Педагогический потенциал учебно-познавательных задач: учебно-методическое пособие. – СПб.: СПбАППО, 2010. – 74 с.

2. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя / под ред. А.Г. Асмолова. – М.: Просвещение, 2010. – 159с 

3. Концепции стандартов второго поколения для основного общего образования.– http://standart.edu.ru

4. Вахрушева А.А., Д.Д. Данилов Как готовить учителей к введению ФГОС // Начальная школа: плюс до и после. - № 5, 2011, с. 12-15.