- Подробности
- Просмотров: 4226
Епифанова Ольга Ивановна,
учитель математики, ГБОУ Петергофская гимназия императора Александра II
Методическая разработка урока алгебры
для 7 класса по теме «Решение задач с помощью систем уравнений»
Данная методическая разработка, посвящена первому уроку в разделе «Решение задач с помощью систем уравнений». Она направлена на знакомство учащихся с новым способом решения текстовых задач. Может быть полезна учителям математики, работающим в классах среднего и высокого уровня подготовки.
Цели урока: актуализация и обобщение способов решения систем линейных уравнений с двумя переменными, знакомство с новым способом решения текстовых задач.
Планируемые результаты:
- предметные:умение в процессе реальной ситуации использовать навыки выраженияодних переменных через другие и применения различных способов решения систем уравнений; овладение навыком составлениясистемы уравнений по тексту задачи в разнообразных интерпретациях;
- метапредметные: умение обрабатывать текстовую информацию и переводить в математическую модель; формирование коммуникативной компетенции обучающихся; умение работать индивидуально и в парах;
- личностные:проявление воли и настойчивости для достижения конечных результатов; выработка уверенности во взаимоотношениях с людьми; формирование устойчивой мотивации и сознательного отношения к учебе, развитие творческих способностей;умение контролировать и оценивать процесс и результаты своей деятельности, свое эмоциональное состояние;
Задачи урока:
- образовательные: способствовать осознанному усвоению навыка составления системы уравнений для решения текстовых задач, закреплению навыков применения различных способов решения систем уравнений;
- развивающие:развитие навыков самостоятельной работы, повышение познавательного интереса, проверить уровень самостоятельной деятельности обучающихся по применению знаний в различных ситуациях,
- воспитательные:формированиекультуры учебного труда, внимательности и точности при выполнении вычислений, формирование адекватной самооценки.
Образовательные технологии, используемые на уроке.
- Здоровьесберегающие технологии: минута психологической разгрузки, правильная осанка при записи, освещение класса.
- Игровые: исторические факты, решение логических задач.
- Индивидуального обучения, парной работы.
Формы работыобучающихся: индивидуальная, групповая, фронтальная.
Методы работы:
- методы организации учебно-познавательной деятельности: словесный, наглядный, практический, самостоятельная работа, работа под руководством;
- методы контроля и самоконтроля: устный опрос, фронтальный опрос, письменный контроль, тест, взаимный контроль, самоконтроль.
Оснащение урока:доска, компьютер, проектор, мультимедийнаяпрезентация, раздаточный материал с заданиями.
План урока.
1. Организационный момент.Сообщение темы и целей урока.
2. Устная работа, выполнение тестовой работы.
3. Актуализация опорных знаний и умений учащихся.
4. Минута психологической разгрузки.
5. Изучение нового материала.
6. Закрепление навыка решения задач с помощью системы уравнений
7. Подведение итогов урока. Рефлексия. Самооценка.
8. Домашнее задание.
Этапы урока.
Перед уроком на доске написать высказывания великих математиков о математике,не подписывая их.
– «Математика – мощный и универсальный метод познания природы, образец для других наук» (Рене Декарт)
– «Любую задачу можно свести к математической, любую математическую задачу можно свести к алгебраической системе уравнений. А любую систему можно свести к решению одного уравнения»(Рене Декарт)
– «Предмет математики настолько серьёзен, что полезно, не упуская случая, сделать его немного занимательным» (Блез Паскаль)
Организационный момент (1 мин). Приветствие учащихся, организация внимания, создание позитивного настроя, проверка готовности рабочих мест и учащихся к уроку, контроль санитарно-гигиенических условий работы: уровень освещённости и т.п.
Учитель. (Слайд 1.)– Здравствуйте, ребята! Проверьте свою готовность к уроку. Откройте тетради, запишите: число, классная работа. Тема урока: «Решение задач с помощью системы уравнений». Целями сегодняшнего урока являются: закрепить навык решения систем уравнений различными способами;познакомиться с новым способом решения текстовых задач.
Устная работа. (7 мин, включая проверку)(Слайд 2.)

Учитель. В качестве разминки предлагаю выполнить тестовое задание. Задания на слайде и в раздаточном материале на партах. Впишите в таблицу буквы, соответствующие правильным ответам. Приступайте к выполнению задания, у вас 5 минут. Затем проверим его выполнение.
Задание теста.
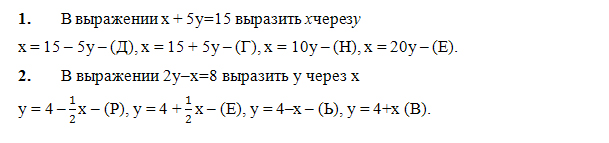
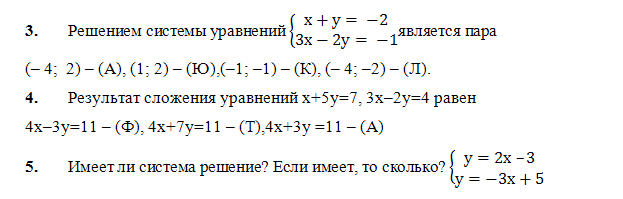
Не имеет – (И), имеет единственное решение – (Р), имеет бесконечное множество решений – (О).
6. Если графики прямых параллельны, то система имеет решение:
Единственное – (К), бесконечное множество решений – (Н), не имеет решений – (Т).
Проверка осуществляется с помощью (Слайда 3.)
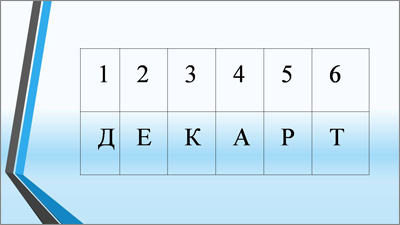
Учитель. Получилось слово «ДЕКАРТ». Поставьте на полях в тетрадях «+», если задание выполнено верно. Поднимите руки, у кого все получилось. Теперь поднимите руки, кто допустил ошибки.
Учитель. (Слайд 4.)

Рене Декарт – это французский математик, философ, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики. Он дал понятия переменной величины и функции. В своей работе «Рассуждение о методе» («Рассуждение о методе, позволяющем направлять свой разум и отыскивать истину в науках») в 1637 году, дал научное описание прямоугольной системы координат. Поэтому прямоугольную систему координат называют также — Декартова система координат. Р. Декарт считал: «Математика — мощный и универсальный метод познания природы, образец для других наук».
Актуализация опорных знаний и умений учащихся (10 мин) (Слайд 5.)

Учитель. Но чтобы использовать математику для изучения процессов природы надо владеть ею.
Постройте Декартову систему координат на треть страницы. За единичный отрезок выберите 1 клетку.
Вопрос 1. Что такое система уравнений? Сколько уравнений? Сколько переменных?
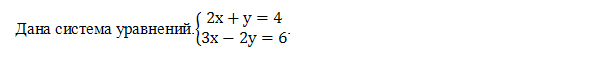
Вопрос 2. Какие способы решения систем уравнений вы знаете?
На слайде появляются способы решения систем уравнения.
Решите данную систему различными способами: 1 вариант – способом подстановки, 2 вариант – способом сложения. На выполнение задания 5 минут.
Учитель. Обменяйтесь тетрадями и проверьте правильность выполнения задания. Опора на слайд (Слайд 6.)

Поставьте на полях знак «+» если задание товарищем выполнено абсолютно верно. Верните тетради.Отметьте полученную точку на координатной плоскости. Слайд 7.
Вопрос 3. Сформулируйте алгоритмы способа подстановки и способа алгебраического сложения.
Слайд 8. Способ подстановки: 1) в одном из уравнений выразить одну переменную через другую; 2) полученное выражение подставить в другое уравнение системы и решить полученное уравнение с одним неизвестным; 3) подставить найденное значение переменной в выражение из пункта 1) и найти значение второго неизвестного.

Слайд 9.Способ сложения: 1)уравнять модули коэффициентов при одном из неизвестных; 2) сложить или вычесть полученные уравнения и найти одно неизвестное; 3) подставить найденное значение неизвестного в одно из уравнений исходной системы.

Психологическая разгрузка. (3 минуты)
Учитель. «Предмет математики настолько серьёзен, что полезно, не упуская случая, сделать его немного занимательным» (Блез Паскаль). Предлагаю вам выполнить задание, которое вас немного отвлечет и развлечет. Слайд 10.

Решите задачу (Слайд 11): как из пяти кусков цепи по 3 звена в каждом собрать цепь из пятнадцати звеньев, сделав только три распила? (Ответ: необходимо распилить три звена одного куска, и полученными звеньями соединить оставшиеся четыре звена).

Поставить «+» тем детям, которые справились с заданием.
Изучение нового материала. (до 12 мин.)
Учитель. Уметь решать системы линейных уравнений – это очень хорошо, но само по себе решение систем уравнений - это лишь метод для более сложных задач. С помощью систем уравнений можно решать различные текстовые задачи, которые встречаются нам в жизни. Именно Декарт считал, что любую задачу можно свести к математической, любую математическую задачу можно свести к алгебраической системе уравнений. А любую систему можно свести к решению одного уравнения.
И теперь и мы, подобно Декарту, будем учиться решать задачи с помощью систем уравнений.
Слайд 12. Задача. Длина прямоугольника на 5 см больше его ширины, а периметр прямоугольника равен 22 см. найдите длину и ширину прямоугольника.

Учитель.Работая в парах, в течение 2-х минут обсудите какие переменные и сколько их можно ввести. Какие уравнения можно составить по условию задачи.
Далее идет составление системы уравнений по тексту задачи с опорой на слайды. (Слайды 13-14)


По ходу обсуждения, на слайде высвечиваются записи, которые учащиеся записывают в тетрадь.
Пусть х см – длина прямоугольника, а у см – ширина прямоугольника.
Так как длина прямоугольника на 5см больше ширины, то можно составить первое уравнение: х – у = 5 (1).
Так как периметр прямоугольника равен 22 см, то составим второе уравнение 2(х + у) = 22 (2).
Так как эти условия выполняются одновременно, то составим и решим
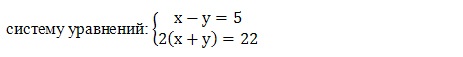
Учитель. Решите систему уравнений различными способами: 1 вариант - способом сложения, 2 вариант – способом подстановки.
Пригласить к доске 2-х учащихся и на обратных сторонах решить данную систему различными способами.
Самопроверка. Решение системы учащимися на доске.
Учитель. Поставьте «+» на полях, если вы решили правильно систему уравнений. Отметьте в системе координат полученную точку.Слайд 15.
Закрепление навыка решения текстовых задач с помощьюсистемы уравнений. (до 10 мин).
Учитель. Слайд 16. В конце урока мы будем подводить итоги и выставлять оценки в соответствии с набранным количеством «+».

Сейчас вам предстоит самостоятельно выбрать и решить задачу. Задачи разного уровня. Правильное решение первой задачи принесет вам «+», правильное решение второй – «++».Постарайтесь договориться с товарищем по парте и выполнить условие: за одной партой учащиеся не должны решать одну и ту же задачу. (Слайд 17.)Время для решения задачи с помощью системы уравнений и ее оформление – 8 минут

Задача 1. Разность двух чисел равна 3. Сумма первого и удвоенного второго числа равна 15. Найдите эти числа.
Задача 2. У овец и кур вместе 36 голов и 100 ног. Сколько овец и сколько кур?
Разбор решения задач с использованием информации размещенной на слайде. (Слайд 18.)

Отметить на координатной плоскости точку, полученную в результате решения задачи 1. (Слайд 19)
Подведение итогов. Самооценка.Рефлексия. (2 мин)
Учитель. – Какие цели ставились в начале урока?Достигли ли мы их?
– Оцените свою работу на уроке. (Слайд 20.)

«+++++» – «5»
«++++» – «4»
«+++» – «3»
Поднимите руки кто оценил себя на «5» («4», «3»).
Учитель. Понравился ли вам урок? Оцените свое состояние (на полях в тетради нарисуйте соответствующий смайлик) Слайд 21:

– «Было легко, и я справился со всеми заданиями»
– «Были трудности, но я справился с большинством заданий»
– «Было очень трудно, со многими заданиями я не справился»
Если останется время, можно некоторых ребят попросить прокомментировать свои рисунки и оценки.
Домашнее задание. (30 с)
Учитель. Запишите домашнее задание.Спасибо всем за урок.
(Слайд 22.) § 37, № 654, 656.

Дополнительная задача.Игроку было предложено 30 вопросов. За каждый правильный ответ ему начислялось 7 баллов, за каждый неправильный ответ с него снималось 12 баллов. Сколько верных и сколько неверных ответов дал игрок, если он набрал 77 баллов.
Используемая литература:
1) Учебно-методические пособия: Ю.М. Колягин, М.В. Ткачев, Н.Е. Федоров, М.И. Шабунин. Алгебра 7 класс: учебник для общеобразовательных организаций, – М.: Просвещение, 2014.
2) Алгебра. 7 класс: поурочные планы по учебнику Ш.А. Алимов и др. / авт.-сост. Е. Г. Лебедева. – Волгоград: Учитель, 2007.
Приложения:
Задания для урока Решение задач с помощью системы уравнений

Ответы и решения:


